The Magnetite Verwey Transition#
The Verwey transition as succinctly defined by Jackson and Moskowitz (2020) is:
a reorganization of the magnetite crystal structure occurring at a temperature TV in the range 80–125 K, where the room-temperature cubic inverse-spinel structure transforms to a monoclinic arrangement, and many physical properties of the mineral (e.g. electrical resistivity, heat capacity, magnetic susceptibility, remanence and coercivity) change significantly.
Brief summary of the magnetite Verwey transition#
At the Verwey transition temperature (\(T_V \approx 120\,\text{K}\)), magnetite transforms from cubic (\(T > T_V\)) to monoclinic (\(T < T_V\)) symmetry. This transformation is related to changes in crystal symmetry and in cation ordering and is accompanied by dramatic changes in electrical conductivity and heat capacity. At a slightly higher temperature (\(\approx 130\,\text{K}\)), the first magnetocrystalline anisotropy constant (\(K_1\)) changes sign, and at this isotropic point (\(T_i\)) the easy directions of magnetization change from the [111] cubic body diagonals (\(T > T_i\)) to the [001] cube edge directions (\(T_V < T < T_i\)). In the transformation to the monoclinic phase (\(T < T_V\)), one of the cube edge orientations becomes the new \(c\)-axis, the unique easy magnetic orientation. Given the significant change in properties associated with the Verwey transition, it can be readily identified by magnetic measurements. The Verwey transition is widely used for identification of magnetite in natural samples (e.g., Mauritsch & Turner, 1975), cleaning of natural remanence by low-temperature demagnetization (e.g., Ozima et al., 1964; Merrill, 1970; Dunlop, 2003, Feinberg et al., 2011), and recognition of magnetotactic bacteria in sediments (e.g., Moskowitz et al., 1989, 1993), and assessment of cation substitution, oxidation, stress, and pressure within magnetite.
At temperatures above the Verwey transition (\(T_v\)), magnetite is a ferrimagnetic semiconductor, properties which are related to its inverse spinel structure, with the tetrahedral (A) sites occupied by ferrous ions, and the octahedral (B) sites containing both ferrous and ferric ions. The electrical conductivity arises mainly from “electron hopping” between the mixed-valence octahedral ions, and the spontaneous magnetization is due to antiferromagnetic coupling of the A and B sublattices.
At \(T > T_v\), magnetocrystalline anisotropy energy is at a minimum when magnetization is oriented along the <111> cubic body diagonal. However, for magnetite crystals that are not perfectly equant, shape anisotropy dominates so that the easy axis of magnetization prefers to lie in the direction of particle elongation. As T approaches \(T_v\) from above, the cubic magnetocrystalline anisotropy constants (\(K_1\), \(K_2\)) both approach zero, and at ~130K, K\(_1\) changes sign. At this isotropic point, the magnetocrystalline easy axis changes from <111> to <100>, but the crystal structure remains cubic until further cooling to \(T_v\), where it becomes monoclinic.
The c-axis of the monoclinic phase is closely aligned with one of the <100> axes of the cubic phase, and the monoclinic a- and b- axes correspond to face-diagonal orientations of the cubic phase. There is a slight distortion of the cubic lattice, approximately equivalent to an elongation along the cubic <110>, and the monoclinic c-axis makes an angle of about 0.23 degrees with the cubic <100>. In particles larger than a few microns, this spontaneous strain is relieved by the formation of twin domains, effectively monoclinic crystallites, each having its own crystallographic orientation with a c-axis along one of the original cube edges. The monoclinic a-, b-, and c- axes are respectively the hard, intermediate and easy magnetic axes. Because monoclinic magnetocrystalline energy is >> cubic magnetocrystalline energy, it plays a dominant role in controlling magnetization at \(T < T_v\).
See also
For more background on the initial observations and history behind the Verwey transition, the fundamental ideas about magnetite’s structure above and below \(T_v\), and how this structure affects macroscopic physical properties, the reader is encouraged to read: Jackson et al. 2011 IRM Quarterly article Interpretation of Low-Temperature Data Part III: The Magnetite Verwey Transition (Part A).
Field-cooling effects on stoichiometric magnetite below \(T_v\)#
This section is focused on the effects on remanence and susceptibility of cooling in an applied field across the Verwey transition, in both the single-domain and multi-domain case. Understanding these effects facilitates the interpretation of remanence upon warming experiments for both field-cooled (FC) and zero-field-cooled (ZFC) experiments.
Source of text
Text introducing the Verwey transition and on low-temperature magnetite remanence and changes in magnetization upon warming is from the Winter 2011 issue of the IRM Quarterly: Jackson, Mike; Bowles, Julie; Banerjee, Subir. (2011). IRM Quarterly, Volume 21, Number 4 (2009). Interpretation of Low-Temperature Data Part V: The Magnetite Verwey Transition (Part B): Field-Cooling Effects on Stoichiometric Magnetite Below TV. Retrieved from the University Digital Conservancy, https://hdl.handle.net/11299/171316. with edits in 2025 by Nick Swanson-Hysell.
Warming of remanence acquired at \(T < T_v\) {#sec_LTSIRM}#
Remanence acquired in the low-temperature state depends on whether or not the sample was cooled in a field through \(T_v\). These differences motivate experimental designs that enable comparison of low-temperature properties in the field-cooled (FC-LTSIRM) state where remenance was acquired throughout cooling from above to below \(T_v\) and the zero-field-cooled (ZFC-LTSIRM) states where remanence was acquired as a pulse at low-temperature below \(T_v\). When magnetite with such a low-temperature remanence is heated through \(T_v\), remanence is lost as the magnetocrystalline anisotropy changes by a factor of about fifteen, and the easy axis of magnetization typically changes due to the shifting balance between crystallographic and shape control. In multi-domain (MD) particles various additional factors contribute to changes in remanence, and in general the effects of the Verwey transition are more pronounced in larger particles. Let us first consider the single-domain (SD) case.
Single-domain behavior#
Imagine a population of SD magnetite with randomly oriented crystallographic axes, magnetized to saturation, and cooling through \(T_v\) in a 2.5-T applied field (an FC-LTSIRM experiment). To minimize energy, the monoclinic c axis forms in each particle along the cube edge closest to the applied field, and when the field is removed after further cooling, the moment of each particle rotates from the applied field direction into alignment with this easy axis. The remanence acquired by such a population through the FC process is the same as that which would be acquired by isothermal magnetization of randomly-oriented SD particles having cubic anisotropy and easy axes along <100>, i.e., 0.832*\(M_{s}\) (e.g., Dunlop & Özdemir, 1997, eq 11.16).
In contrast, random c-axis selection during an ZFC-LTSIRM experiment yields an isotropic population of monoclinic grains which, when magnetized isothermally in a strong field, acquires a low-temperature SIRM equal to \(0.5*M_{s}\) (the same as the room-temperature SIRM acquired by a population of uniaxial SD particles). The ratio of intensities \(M_{FC}/M_{ZFC}\) for these ideal SD populations at low temperature is therefore 0.832/0.5=1.664. This ratio has been labelled \(R_{LT}\) by Smirnov (2009), who measured it as a function of grain size for magnetites of variable stoichiometry, finding maximum values near 1.3 for his finest-grained samples. Similar results are shown in Figure 7 for silicate grains with magnetite inclusions from the Bushveld complex (J. Feinberg, unpublished data).
We noted above that for particles cooled in the absence of a field, c-axis selection is commonly considered to be a random process. Alternatively, however, it has been suggested (Bickford, 1953; Medrano et al., 1999; Smirnov and Tarduno, 2002; Muxworthy and Williams, 2006; Kasama et al 2010), that ZFC c-axis selection may be influenced or controlled by magnetic moment orientations during cooling through \(T_v\), although to a much lesser degree than for FC. In this case, a c-axis is selected which is closest to the high-temperature (\(T > T_v\)) moment of each individual grain or domain.
Having produced low-temperature FC and ZFC remanent magnetizations, let us now consider what happens while warming them through \(T_v\). A decrease in net magnetization results as individual SD particle moments rotate from one easy axis at low temperature to another at high temperature (Fig. 6). The intensity of remanence remaining above \(T_v\) is the same for both the FC and ZFC cases (since the FC-induced anisotropy disappears, and the distribution of easy-axis orientations is the same as in the ZFC case). The magnitude of the remanence loss when warming through \(T_v\) is related to the relative magnitude of the shape and magnetocrystalline anisotropy energies.
Although at \(T < T_v\) magnetocrystalline anisotropy is dominant, shape is still important and the remanent moment of each SD particle orients itself somewhere between the crystallographic c-axis and the dimensional long axis. Particles with higher aspect ratios will therefore suffer less remanence loss on warming. Numerical models (Carter-Stiglitz et al., 2002) showed that for randomly-oriented particles with weak shape anisotropy, a ZFC low-temperature SIRM loses half its remanence on warming through \(T_v\), and the fractional loss diminishes with increasing elongation, as well as with increasing grain size (also seen in experimental data, Özdemir et al., 2002).
Moskowitz et al. (1993) observed that variation in magnetization across \(T_v\) serves as a diagnostic indicator of magnetosomes in intact chains. For a magnetization acquired at low temperature the fractional loss of remanence on warming across \(T_v\) is defined as \(\delta = (M^{80K} - M^{150K})/M^{80K}\). Moskowitz et al. (1993) observed that the loss for a remanence acquired after cooling in a strong field (\(\delta_{FC}\)) is always greater than that for a ZFC remanence (\(\delta_{ZFC}\)). This, as described above, is expected for all SD populations, biogenic or not, due to the induced anisotropy of the FC state. But notably, Moskowitz et al. (1993) found that the \(\delta\)-ratio (\(\delta_{FC}/\delta_{ZFC}\)) was >2 for intact magnetosome chains and <2 for samples with inorganic SD particles or with disrupted chains. Factors that may be responsible for this signature of bacterial magnetosome chains include that magnetosomes have shape and room-temperature crystallographic easy axes that coincide: they are “manufactured” to be elongated along a <111> axis. Moreover there are strong magnetostatic interactions among neighboring particles in the intracellular chains.
These factors were simulated in numerical models by Carter-Stiglitz et al. (2004), who found that elevated \(\delta\)-ratios can best be explained by non-stoichiometry. While this topic deserves its own deep dive, for the purposes of this section we will note that maghemitization results in a decrease in magnetocrystalline anisotropy at \(T < T_v\), thus resulting in a decreasing \(\delta\) in both FC and ZFC curves. As can be seen in Figure 7, \(\delta_{ZFC}\) is often very low in samples with bacterial magnetite, and consequently the \(\delta\)-ratio can be quite large (up to about 6 in the models of Carter-Stiglitz et al., 2004). The effects of partial maghemitization are greater in the ZFC case, because in the FC case there is an easy-axis bias. Thus, the elevated \(\delta\)-ratios are a sensitive indicator of stable single-domain magnetite, but not conclusively biogenic in origin. Furthermore, experimental and modeling results suggest that magnetosomes become partially oxidized extremely rapidly and/or they may not produce perfectly stoichiometric magnetite.
Multi-domain behavior#
When MD magnetite cools through \(T_v\), the resulting magnetic state is complicated (compared to the SD case) by the presence of both domain walls and transformational twins. Kasama et al. (2010) indicate 24 possible orientational variants, each having the monoclinic c-axis aligned along one of the cubic <100> axes and the monoclinic a-axis along one of the cubic face diagonals perpendicular to c. Twin domains with any of these orientations are separated by twin walls from other twin domains having differing orientations. Various configurations are possible; for example a twin wall may separate domains having different hard (a) axis orientations but identical easy axes, or the wall may be a boundary where two c-axes intersect at right angles. Because of the intense magnetocrystalline anisotropy, the latter type of twin wall is also necessarily a 90° domain wall. Such twin configurations and the resultant immobile domain walls exert strong controls on the low-temperature magnetic properties of magnetite. Kasama et al. (2010) have produced amazing videos of the monoclinic twins nucleating and growing in cubic magnetite as it cools through \(T_v\).
One of the peculiar features of MD magnetite is that in contrast to the SD case, a ZFC low-temperature SIRM has a higher intensity than a FC LTSIRM (Fig. 8). This was first reported by Brachfeld et al. (2001, 2002) and was also observed by Kosterov (2001, 2003) who proposed that the degree of easy-axis alignment with respect to the applied field (at low-T) could lead to lowered coercivity in the FC state. Further work (Carter-Stiglitz et al., 2006; Kosterov & Fabian 2008) suggests that the elevated remanence in the ZFC state arises from the twin boundaries which serve to pin domain walls and produce an effectively smaller magnetic grain size. In the FC case, the formation of twins is suppressed (particularly those with c axes at a high angle to the cooling field) because of the field-induced easy axis selection (described above), resulting in an overall softer magnetization. The 180° domain walls that form in this case are more easily moved than the 90° twin boundaries/ domain walls that form in the ZFC case.
Susceptibility and hysteresis in the FC and ZFC states#
For MD magnetite, the hard wall pinning in the twinned low-temperature state that is responsible for retention of strong ZFC remanence can also be seen in low-field susceptibility and high-field hysteresis measurements as functions of temperature and cooling fields (Kosterov 2003; Carter-Stiglitz et al. 2006; Kosterov & Fabian 2008). The monoclinic phase is significantly harder magnetically in the ZFC state than in the FC state (when measurements are made parallel to the cooling field), having lower susceptibility (Fig. 9), higher coercivity, and higher Mr/Ms ratios.
Pseudo-single-domain case#
Many properties of PSD grains are indistinguishable from those of suitable mixtures of SD and MD grains (e.g.,Dunlop, 2002), and to a large extent the same is also true of simple FC-ZFC remanence experiments. For example, an observed \(R_{LT}\) approximately equal to one could correspond to a mixture of SD (\(R_{LT}\) >1) and MD (\(R_{LT}\) <1) particles, or it could be due to a unimodal distribution of intermediate sized PSD grains. However Smirnov (2006a,b, 2007) has discovered some distinctive PSD behavior at low temperatures in hysteresis and FORC measurements in the FC and ZFC states. In the “field memory effect”, low-temperature hysteresis loops exhibit some distortion in the field range corresponding to the cooling field (several mT to tens of mT) and FORC diagrams exhibit double peaks, roughly symmetric around a horizontal line corresponding to the cooling field. These effects were found only in unimodal populations with sizes in the PSD range; SD and MD populations and mixtures thereof exhibited no “field memory” effects.
Behavior of other minerals in FC-ZFC experiments#
Quantitative measures of Verwey-transition-related behavior can get fouled up by the presence of other remanence-carrying phases in natural samples. Maghemite and greigite have no low-temperature transitions, and when they are thermally stable (larger than the superparamagnetic to stable-single-domain threshold at room temperature) their remanence is almost independent of temperature for T < 300K. A large contribution from either therefore drives \(R_{LT}\) towards 1, and \(\delta_{FC}\) and \(\delta_{ZFC}\) towards zero; the ratio \(\delta_{FC}/\delta_{ZFC}\) nevertheless remains a good indicator of the presence of bacterial magnetite as long as at least 10% of the remanence is carried by intact magnetosome chains (Moskowitz et al., 1993). Things are more troublesome when there are significant contributions from other magnetites (e.g., collapsed chains or detrital populations); in such situations the “bug test” gives a positive result only when 80-90% or more of the remanence is due to magnetosome chains.
Goethite is another villain in the bacterial magnetite story. It has no low-temperature transition, but there is usually a very large difference between FC and ZFC remanences due to the combination of very high coercivity and relatively low ordering temperature (~400K; Özdemir and Dunlop, 1996). Isothermal strong-field magnetization at 10K or 20K is quite ineffective at producing a strong remanence in the ZFC state in this very hard material, even when 2.5 T is applied; cooling in the same field from 300K magnetizes much more efficiently through the combined thermal and magnetic field energies, in effect producing a strong-field pTRM. \(R_{LT}\) is commonly 5 or more, and \(\delta_{FC}\) can sometimes be larger for pure goethite than for pure bacterial magnetites.
Low-Temperature Demagnetization of Stoichiometric Magnetite#
This section addresses the Verwey transition in the context of a common experiment performed at the Institute for Rock Magnetism which is low-temperature cycling of a remanence acquired at room-temperature. The section is focused on discussion of the behavoir of stoichiometric magnetite. Note that cation substitution, oxidation, stress, and pressure effects can all result in variable deviations from this behavior that are not covered in this section.
Source of text
This text in this section on the low-temperature demagnetization of magnetite during cooling is from the Summer 2012 issue of the IRM Quarterly: Bowles, Julie; Jackson, Mike; Banerjee, Subir. (2012). IRM Quarterly, Volume 22, Number 2 (Summer 2012). Cover article: Interpretation of Low-Temperature Data Part VI: The Magnetite Verwey Transition (Part C): Low-Temperature Demagnetization of Stoichiometric Magnetite. Retrieved from the University Digital Conservancy, https://hdl.handle.net/11299/171327. with minor edits by Nick Swanson-Hysell.
Low-temperature demagnetization (LTD) of magnetite (by cycling a sample from room temperature to a temperature \(T < T_V \sim122K\) and back, in zero field) has along and distinguished history (e.g., Ozima et al., 1964 Kobayashi & Fuller, 1968; Merrill, 1970). Despite many years of study, however, LTD still retains some significant mysteries. In contrast to the warming of low-temperature remanences (section sec_LTSIRM), where properties change abruptly and dramatically when the strong monoclinic magnetocrystalline anisotropy vanishes at \(T_v\), the changes on cooling from room temperature can be more gradual, subtle and complex: the weak cubic magnetocrystalline anisotropy diminishes progressively until the easy axis orientation changes at the isotropic point \(T_K \sim130K\) (from body diagonal to cube edge), and finally the monoclinic phase nucleates at \(T_v\) and propagates through the individual particles. Moreover, the initial state for LTD experiments is often subtle and complex as well (natural remanence, or weak-field lab analogues), whereas FC/ZFC experiments typically involve brute-force strong-field remanences. For these reasons, the behavior we observe during zero-field cooling and rewarming can exhibit a rich variety of features.
For many years there were practical hurdles to measuring magnetization during complete cooling/warming cycles. Commonly the effects of low-temperature cycling were studied solely through measurement of remanence at room temperature, before and after treatment by immersion in liquid nitrogen in a zero-field environment (e.g., Merrill, 1970). Some of the key early observations of magnetization during cooling/warming cycles (Yama-ai et al., 1963; Nagata et al., 1964; Ozima et al., 1964; Kobayashi & Fuller, 1968) involved the newly-developed vibrating-sample magnetometer (Flanders and Doyle, 1962). Later work involved continuous measurements on specialized instruments including a Dewar-equipped spinner magnetometer (Hartstra, 1983) and a SQUID susceptometer (Halgedahl & Jarrard, 1995). Until about 1998 at the the Institute for Rock Magnetism, the Quantum Designs MPMS instruments were unable to measure during cooling, due to hardware and software limitations (IRMQ v. 8, n. 4; Özdemir & Dunlop, 1999). Prior to that time, all low-temperature experiments at the IRM were based solely on measurements during warming. In the time since, the community has accumulated a large body of data on the behavior of magnetite-bearing materials during complete low-temperature cycles (e.g., Fig. 9).
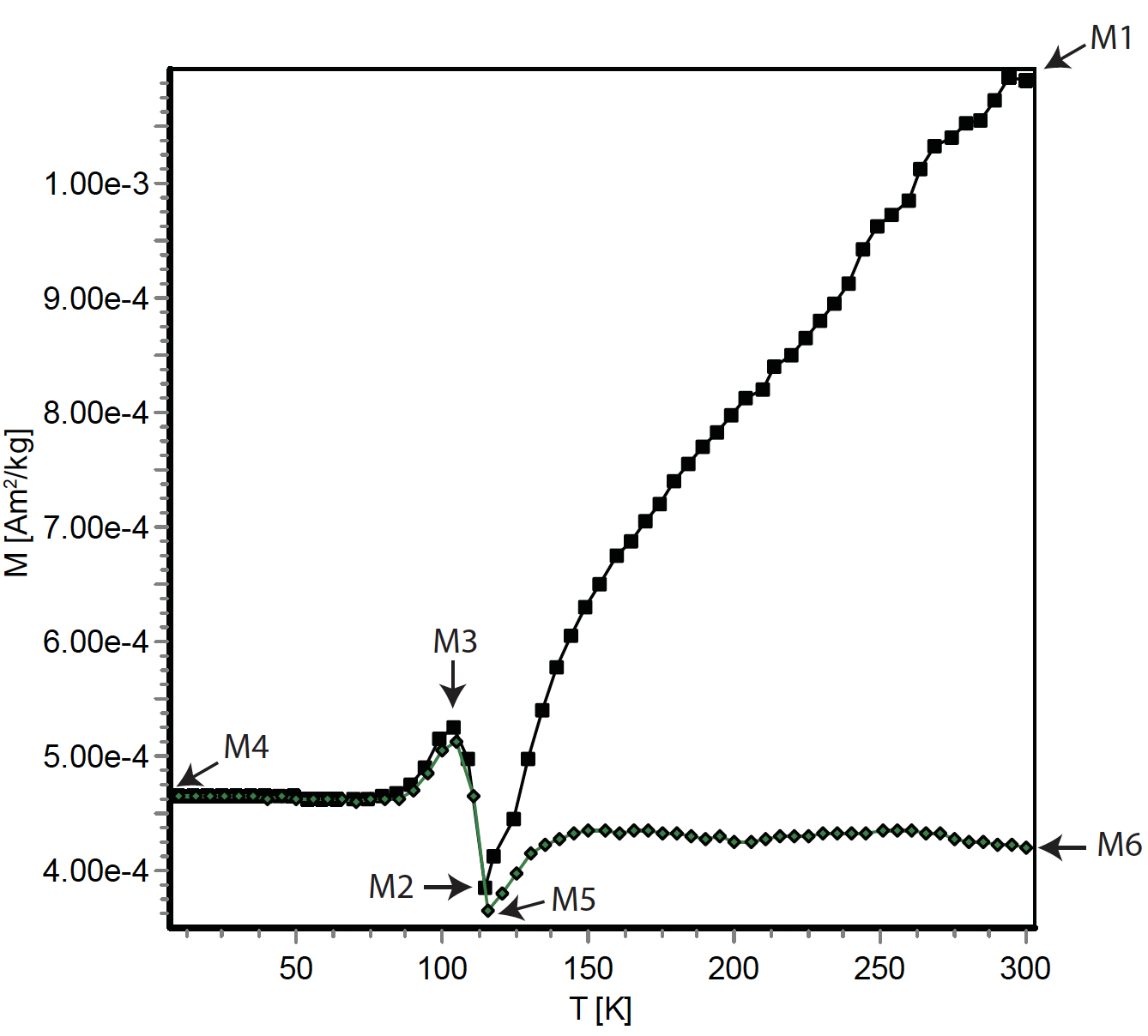
Fig. 9 Anatomy of a low-T cycle of RTSIRM (initial magnetization M1). Black squares show cooling curve reaching a minimum (M2) at or near T\(_v\), followed by an increase to a local maximum M3 and subsequent decline to M4 at the minimum temperature (in this case 10 K). On rewarming (green diamonds) the path retraces the cooling curve through M3 and M2 and reaches a slightly lower minimum (M5) before recovering somewhat on returning to M6 at room temperature (unpublished data from P Kelso, granite from the Idaho Batholith). Note that not all of these features are generally seen in RTSIRM low-T cycles; for many/most natural magnetites, M5≈M4≈M3≈M2. Many parameters have been introduced to describe behavior during such experiments. The simplest is often called the “memory ratio,” equal to M6/M1, i.e., the proportion of initial remanence that survives the low-T cycle (e.g., Dunlop & Argyle, 1991; Muxworthy & Williams, 2006). This can be determined without measurements at low T, and is therefore readily quantified. The same quantity is called ‘second memory’ by Özdemir et al (2002), to distinguish it from ‘first memory’ (=M4/M1), the proportion of RTSIRM that survives the first crossing of the transition. King & Williams (2000) define “memory” as the magnetization recovered on rewarming through the transition, i.e., M6–M5. For cases where there is a distinct jump in remanence on crossing the transition, the parameter ΔVJ (Muxworthy et al, 2003) is defined as size of the discontinuity, normalized to the initial remanence, i.e., ΔVJ =(M3–M2)/M1; it can have positive values (as in the figure) or negative values. Other parameters known as ΔMm and ΔMc (Özdemir & Dunlop 2010) respectively denote magnetization differences in the monoclinic and cubic phases: ΔMm = M4–M5, and ΔMc = M1–M6.#
Pioneering studies#
The earliest studies of changes in room-temperature remanence during low-temperature cycles were designed to understand: (a) the fundamental origins of stable remanence in multidomain grains and the relative importance of stress, microstructures, magnetocrystalline anisotropy and particle geometry, and (b) the nature of the low-temperature transitional phenomena themselves. In particular, for many years there was no clear evidence to show the relative importance of the magnetocrystalline anisotropy transition and the Verwey transition in low-temperature demagnetization (Halgedahl & Jarrard 1995; Özdemir & Dunlop, 1999; Dunlop, 2003, Liu & Yu, 2004). Three notable properties of magnetite’s LTD behavior were noted almost immediately (e.g., Ozima et al., 1964; Kobayashi & Fuller, 1968; Merrill, 1970):
multidomain grains are demagnetized much more effectively than single-domain grains
strong-field remanence is erased to a much greater extent than weak-field remanence (such as thermal remanent magnetization)
multiple low-temperature cycles generally demagnetize more completely than a single cycle. Kobayashi & Fuller (1968) speculated that the origin of “memory” (the remanence that survives LTD) is related to the origin of TRM. Ozima et al (1964) showed experimentally that soft (1-10 mT) isothermal remanent magnetizations (IRMs), superposed on TRM or NRM, could be preferentially removed by low-temperature zero-field treatments. Yama-ai et al (1963) observed a phenomenon that we have never seen reproduced, namely a reversal of magnetization in a single crystal on cooling through 130 K, followed by a return to the original polarity on rewarming, and they hypothesized a mechanism involving two sources of magnetization, weakly coupled magnetostatically, since the self-reversal could be suppressed by application of a weak field during cooling. Kobayashi & Fuller (1968) carried out several experiments to test this idea further, including: (a) comparison of room-temperature AF demagnetization spectra of RTSIRM and of “memory” after LTD, showing that the latter has much higher stability, and (b) superposition onto a room-temperature SIRM of a soft reverse-polarity low-temperature IRM, showing that “memory” is independent of the soft low-temperature overprint. They argued that a magnetostatic model could not explain these observations and that internal stresses must play a key role.
Effects of Domain State#
Single Domain, low-temperature cycling of RTSIRM#
In an SD particle at \(T > T_v\), magnetic remanence lies along a minimum-energy orientation between one of the cubic <111> easy axes and the axis of particle elongation; the precise orientation depends on the relative strengths of the magnetocrystalline anisotropy and the shape anisotropy, the latter usually being stronger. On cooling through the isotropic point at \(T_K = 130K\), the cube edge orientations <100> become the magnetocrystalline easy axes, and then with the crystallographic change at \(T_v = 120K\), the monoclinic c-axis [001] becomes the strongly-preferred orientation of magnetization, regardless of grain shape. It has been commonly thought that in the absence of an applied field or magnetostatic interactions, one of the cube edge orientations is chosen at random to become the monoclinic c-axis. Rotation of the individual particle moments into c-axis alignment causes a loss of room temperature remanence, as some of the magnetization is effectively randomized (e.g. Fig. 3a,b,c). If there is no systematic relationship between crystallography and grain shape, the change from one uniaxial anisotropy to another results in a decrease of up to 50% in the net remanence of a population of grains. When the sample is reheated, the moments might be expected to rotate reversibly back to their original direction with little to no loss of the original remanence . This appears to be true for some samples dominated by SD shape anisotropy at \(T > T_v\) (e.g., Fig 3c), because there are only two easy axes to choose from on re-heating; the shortest rotation path will almost always be a return to the starting room-temperature direction. Perfect reversibility is rarely seen in nature, however, and for particles with small degrees of elongation (<1.15) it has been argued (Muxworthy and Williams, 2006) that cubic anisotropy indeed plays a role at \(T > T_v\): the moment will find some orientation that is a local minimum in the sum of magnetocrystalline anisotropy energy (3 easy axes below \(T_K\) and 4 above) and magnetostatic (shape anisotropy) energy (2 or more easy directions). Not all of the individual particle moments return to their original orientations, and therefore there is incomplete recovery of remanence. This was demonstrated experimentally as early as 1978 when Levi and Merrill (1978) measured TRM remanence before and after cycling to T < 130K. They found that remanence recovery was greater in acicular grains than in equant grains. Likewise, interparticle magnetostatic interactions have been modeled to have a similar effect (Muxworthy and Williams, 2006), and can additionally reproduce intriguing features such as an additional decrease in M (rather than recovery) on warming back through \(T_v\) (Fig 3b).
Multi-domain, low-temperature cycling of RTSIRM#
In contrast to the SD case, remanence within the domains of larger particles almost always lies along one of the cubic <111> axes for \(T > T_v\). On cooling, the magnetocrystalline anisotropy energy decreases and domains reorganize irreversibly even at temperatures well above \(T_K\) (Halgedahl & Jarrard 95; Dunlop 2003; Liu and Yu 2004). For true MD populations (20 um and larger), 80% or more of RTSIRM can be erased by cooling to temperatures approaching but not reaching TK. On cooling through the isotropic point, the cubic magnetocrystalline easy axes change to <100>. Instead of coherent rotation of magnetization as in the SD case, the room-temperature domain configurations become unstable and walls may begin to move or dissolve, while new walls are nucleated. However in the temperature interval between \(T_K\) and \(T_v\), the magnetocrystalline anisotropy remains weak, and only rarely is there a direct visible indication of \(T_K\) in remanence cooling curves (Fig 4; Özdemir & Dunlop, 1999). Similarly, Kasama et al (2012) saw no significant changes in domain arrangements in images obtained by Lorentz microscopy above and below \(T_K\).
It is at \(T_v\), with a tenfold increase in magnetocrystalline anisotropy and a change from cubic to monoclinic symmetry, that domain reorganization is most forcefully driven. MD grains are large enough for the monoclinic phase to nucleate and begin growing in multiple regions independently of one another, with c-axis selection determined (in zero applied field) either randomly, or by local stress fields, or by inheritance of the cubic-phase domain-moment orientations. Kasama et al (2012) observed strong similarities in the domain configurations above \(T_v\) and below it after cooling in zero field, indicating some control of the monoclinic c-axis selection by the pre-existing local magnetization (as suggested by Bickford in 1953). For samples containing large MD grains, and especially for single crystals, the remanence often “jumps” on cooling through \(T_v\) in zero field (Özdemir & Dunlop, 1999; Muxworthy et al., 2003); the magnitude of the increase depends on the nature of the initial remanence as well as on particle size. Changes in remanent magnetization on cooling and rewarming below \(T_v\) are almost always slight and perfectly reversible.
As the sample is warmed back through \(T_v\) , the strong monoclinic anisotropy abruptly vanishes, as does the monoclinic twinning, and domain walls will again unpin and reform. The c axis of each monoclinic twin domain becomes one of the cubic <100> easy axes, so there is no moment rotation required by the change in magnetocrystalline anisotropy, but its diminished strength shifts the balance towards shape and magnetoelastic anisotropies. It is interesting that any “jump” in remanence associated with \(T_v\) is generally almost perfectly reversible, i.e., M5~M2 (Fig 4).
On continued warming through \(T_K\), the K1 anisotropy constant again changes sign and the cubic body diagonals again become the magnetocrystalline easy axes. There is no reason for the domains to reform precisely in the original room-temperature configuration, but Kasama et al (2012) have observed significant similarities in the patterns at 143 K before and after zero-field cycling through \(T_v\) . Nevertheless, in MD magnetites there is typically little or no recovery of the remanence lost on cooling. The “memory ratio” (M6/M1) decreases systematically with increasing grain size from SD through MD grain sizes (Merrill, 1970; Levi and Merrill, 1978; Heider et al., 1992). Halgedahl and Jarrard (1995) found a nearly linear relationship between the memory ratio and the logarithm of grain size and, therefore, the number of domains.
It has frequently been suggested that this memory ratio can therefore be used to estimate grain size, but such an interpretation is predicated on the assumption of stoichiometric magnetite. This cannot be assumed in many natural samples which will frequently have at least a small degree of cation deficiency or cation-substitution, both of which can have a strong affect on the memory ratio. Moreover the memory ratio in natural materials with mixed mineralogy depends on the relative proportions of phases that are invulnerable to LTD, and so granulometric estimation is inseparable from the more general unmixing problem. Additionally, as noted above, in the SD/PSD grain size region, acicular magnetite is found to have a higher memory ratio than comparably-sized equant grains.
A final complication in the interpretation of MD LTD memory lies in crystal defects and associated stress fields, which may serve as barriers to domain wall motion or as sites for wall re-nucleation, and which may thereby help to transfer magnetically-stored information back and forth between the cubic and monoclinic phases (Kobayashi and Fuller, 1968; Hodych, 1991; Heider et al 1992; Hodych et al., 1998; Kasama et al., 2012). Thus, the memory is a function of not only grain size but also stoichiometry and defects/stresses. Because LTD memory depends on these factors, it is not surprising that it also depends on the nature of the initial remanence.
LTD of Different Remanences; Coercivity and#
Unblocking-temperature Spectra after LTD
Is it possible to isolate primary thermoremanence by selectively demagnetizing viscous and other overprints using LTD? Can the portion of NRM carried by MD grains be selectively removed by low-temperature treatments, leaving an ideal SD-carried remanence for paleointensity or paleothermometry studies? The answer to these is an unequivocal “Yes, to a certain extent, but…” Interest in the use of LTD to isolate the primary TRM carried by SD grains has of course been particularly strong in connection with paleointensity, where only such ideal records are amenable to techniques such as the Thellier-Thellier method, which depend on the laws of pTRM additivity, independence and reciprocity. Many studies have shown that the remanent “memory” of TRM and pTRM (and their anhysteretic analogues) after LTD have more SD-like properties than the untreated thermoremanences, including closer adherence to the virtuous properties of additivity, independence and reciprocity, but LTD pretreatments still commonly fail to yield reliable paleointensities from samples with MD magnetite (Dunlop & Argyle, 1991; Heider et al, 1992; McClelland et al., 1996; Shcherbakova et al., 1996; Muxworthy, 2000; Muxworthy & McClelland 2000a,b; Yu et al 2003; Yamamoto et al 2003; Borradaile et al., 2004; Dunlop et al., 2005).
Multicycle LTD#
Erasure of magnetic information by a single cycle through \(T_v\) is imperfect; some fraction is remembered in spite of the randomness inherent in phase nucleation, c-axis selection, domain nucleation, etc. Liu and Yu (2004) found experimentally that remanence decays exponentially with the number of LTD cycles, to a nonzero level that depends on the temperature endpoints of the LTD cycles, as well as on all the usual other factors like particle size and type of remanence. The first cycle is responsible for more than 75% of the total remanence loss caused by 10 or more LTD cycles, when the cycles cross \(T_K\) but not \(T_v\). For lower-temperature cycles that cross \(T_v\) but not \(T_K\), the first cycle accounts for about half the total demagnetization accomplished by 10 or more cycles. Liu and Yu (2004) modeled the process using a “Boltzman analog” approach involving both domain reorganization above \(T_K\) and easy-axis reorientation through \(T_K\) and \(T_v\).
Experimental Artifacts#
No article on the fine details of low-temperature magnetic behavior would be complete without some mention of various nefarious experimental artifacts that torment and bedevil those at the IRM on a regular basis, by mimicking and/or distorting the signatures of the Verwey transition and other significant features. In the context of LTD, the most bothersome issue involves spurious abrupt decreases in remanence while cooling in zero field, due to reorientation of particles in powder samples or other similar effects. Typically, these appear as discontinuous steps superposed on a smoothly changing signal (e.g., Fig. 10). With surprising frequency, the anomalous drops occur within the temperature ranges where we look for the Morin transition (hematite), the Verwey transition, the Besnus transition (pyhrrotite), or different mineral isotropic points, and it can be difficult to evaluate their significance. Repeat runs commonly show that they are not reproducible in detail, or often even in gross form; repacking the sample more tightly to immobilize the particles more completely in many cases eliminates the artifacts. It is conceivable that particle reorientation is itself related in some way to the phase transitions, and the abrupt drops may still in some cases be a guide to the presence of transitions. However, in order to obtain unambiguously interpretable results we recommend, when practical, working with solid rock chips/slices, or mixing granular materials with a compressible binder to reduce or eliminate the occurrence of such gremlins.
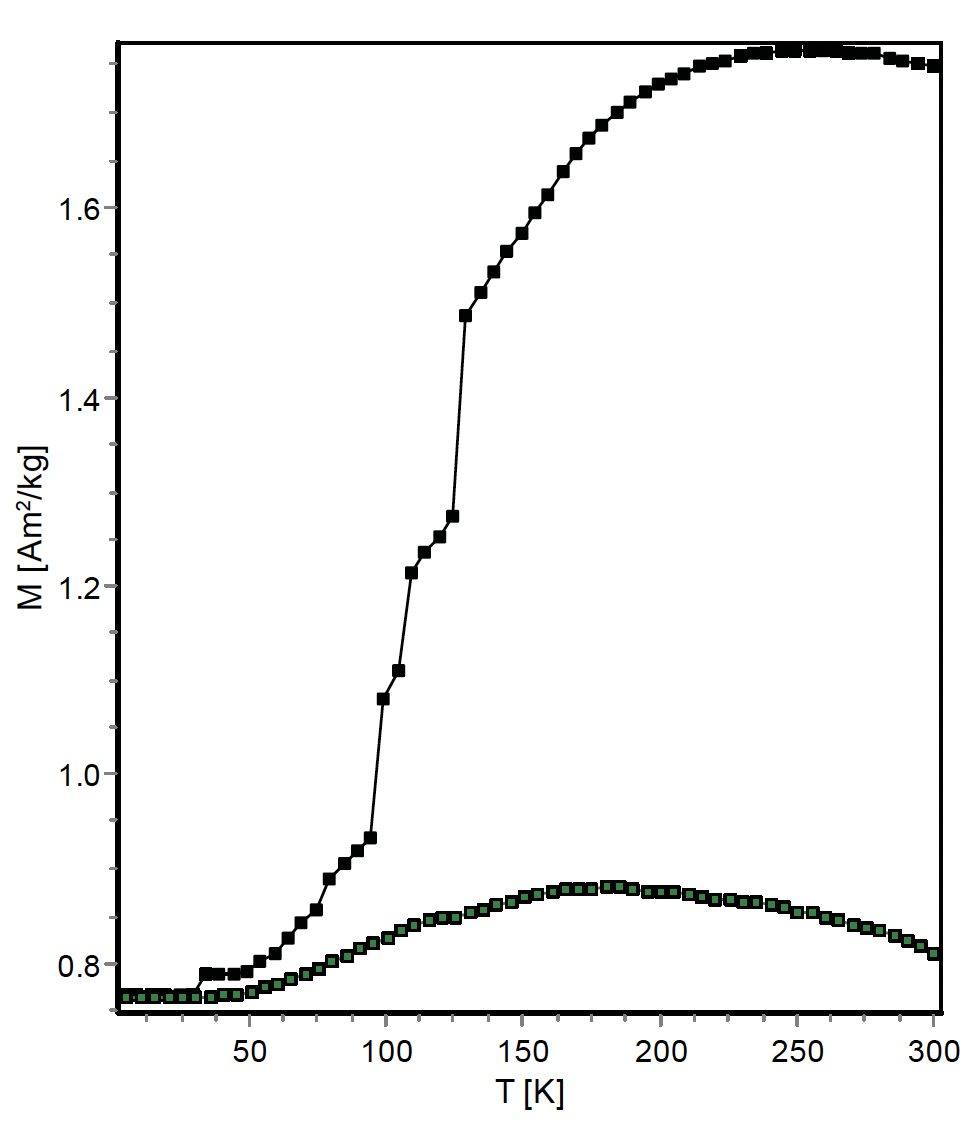
Fig. 10 Frustrating inexplicable mystery discontinuities commonly found in cooling curves on powder samples, often tantalizingly close to significant transition temperatures. Repacking and remeasuring sometimes eliminates these.#
Closing Remarks#
In the nearly fifty years that have passed since the first work on LTD, it has continued to draw interest and stimulate research, even if it has not quite become a staple of paleomagnetism in the same way that thermal and alternating-field demagnetization methods are. Stepwise LTD (e.g. Dunlop 2003) and full 3-axis magnetization measurements during low-temperature cycles (Bowles et al, 2010; Smirnov & Tarduno, 2011) promise to improve our understanding of natural and artificial remanences carried by magnetite, and direct imaging of cubic and monoclinic crystallographic and magnetic microstructure (Kasama et al., 2012) will continue to clarify their interdependent changes across \(T_v\), deepening our understanding of transition-related phenomena as well as of the stabilizing mechanisms of room-temperature remanence. Behavior of room-temperature remanence during LTD provides information on the mineralogy, grain sizes, stoichiometry and anisotropy of the carriers, and for these reasons magnetization measurements across low-temperature transitions have become, and will continue to be, essential for studying the sources (minerals and mechanisms) of stable remanence in natural materials.
References#
Abe, K., Y. Miyamoto, and S. Chikazumi (1976), Magnetocrystalline anisotropy of low temperature phase of magnetite, J. Phys. Soc. Japan, 41,1894-1902.
Bickford, L. R., Jr. (1953), The low temperature transformation in ferrites, Rev. Mod. Phys., 25, 75–79
Brachfeld, S., Y. Guyodo, and G.D. Acton (2001), Data report: The magnetic mineral assemblage of hemiplagic drifts, ODP Site 1096, In Barker, P.F., Camerlenghi, A., Acton,G.D., and Ramsay, A.T.S. (Eds.), Proc. ODP, Sci. Results, 178, 1–12
Brachfeld, S.A., S.K. Banerjee, Y. Guyodo, G.D. Acton (2002), A 13200 year history of century to millennial-scale paleoenvironmental change magnetically recorded in the Palmer Deep, western Antarctic Peninsula, Earth Planet. Sci. Lett., 194, 311-326.
Carter-Stiglitz, B., B. Moskowitz, P. Solheid, T.S. Berquó, M. Jackson, and A. Kosterov (2006), Low-temperature magnetic behavior of multidomain titanomagnetites: TM0, TM16, and TM35, J. Geophys. Res., 111, B12S05, doi:10.1029/2006JB004561.
Carter-Stiglitz, B., B. Moskowitz, and M. Jackson (2004), More on the low-temperature magnetism of stable single domain magnetite: Reversibility and non-stoichiometry, Geophys. Res. Lett., 31, L06606, doi:10.1029/2003GL019155.
Carter-Stiglitz, B., M. Jackson, and B. Moskowitz (2002), Lowtemperature remanence in stable single domain magnetite, Geophys. Res. Lett., 29. (See also correction v.30, n.21, 2113, 2003)
Dunlop, D.J. (2002), Theory and application of the Day plot (Mrs/Ms versus Hcr/Hc) 1. Theoretical curves and tests using titanomagnetite data, J. Geophys. Res., 107, doi: doi:10.1029/2006JB004561.
Dunlop, D.J., and Ö. Özdemir (1997), Rock Magnetism: Fundamentals and frontiers, Cambridge University Press, New York, 573pp.
Kasama, T., N.S. Church, J.M. Feinberg, R.E. Dunin-Borkowski, and R.J. Harrison (2010), Direct observation of ferrimagnetic/ ferroelastic domain interactions in magnetite below the Verwey transition, Earth Planet. Sci. Lett., 297, 10-17.
Kosterov, A. (2001), Magnetic hysteresis of pseudo-single-domain and multidomain magnetite below the Verwey transition, Earth Planet. Sci. Lett., 186, 245-253.
Kosterov, A., (2003), Low-temperature magnetization and AC susceptibility of magnetite: effect of thermomagnetic history, Geophys. J. Int., 154, 58-71.
Kosterov, A., and K. Fabian (2008), Twinning control of magnetic properties of multidomain magnetite below the Verwey transition revealed by measurements on individual particles, Geophys. J. Int., 174(1), 93-106
Li, C. H. (1932), Magnetic properties of magnetite crystals at low temperature, Phys. Rev., 40, 1002-1012.
Medrano, C., M. Schlenker, J. Baruchel, J. Espeso, and Y. Miyamoto (1999), Domains in the low-temperature phase of magnetite from synchrotron-radiation x-ray topographs, Phys. Rev. B., 59, 1185-1195.
Moskowitz, B.M., R.B. Frankel, and D.A. Bazylinski, Rock magnetic criteria for the detection of biogenic magnetite, Earth Planet. Sci. Lett., 120, 283-300, 1993.
Muxworthy, A.R., and W. Williams (2006), Low-temperature cooling behavior of single-domain magnetite: Forcing of the crystallographic axes and interactions, J. Geophys. Res., 111, B07103, doi:10.1029/2006JB004298.
Özdemir, Ö., and D.J. Dunlop (1996), Thermoremanence and Néel temperature of geothite, Geophys. Res. Lett, 23, 912-924.
Özdemir, Ö., D.J. Dunlop, and B.M. Moskowitz, Changes in remanence, coercivity and domain state at low temperature in magnetite, Earth Planet. Sci. Lett., 194, 343-358, 2002.
Smirnov, A.V., and J.A. Tarduno (2002), Magnetic field control of the low-temperature magnetic properties of stoichiometric and cation-deficient magnetite, Earth Planet. Sci. Lett., 194, 359-368.
Smirnov, A. V. (2006a), Memory of the magnetic field applied during cooling in the low-temperature phase of magnetite: Grain-size dependence, J. Geophys. Res., 111, B12S04, doi:10.1029/2006JB004573.
Smirnov, A. V. (2006b), Low-temperature magnetic properties of magnetite using first-order reversal curve analysis: Implications for the pseudo-single domain state, Geochem. Geophys. Geosys., 7, Q11011, doi:10.1029/2006GC001397.
Smirnov, A. V. (2007), Effect of the magnetic field applied during cooling on magnetic hysteresis in the low-temperature phase of magnetite: First-order reversal curve (FORC) analysis, Geochem. Geophys. Geosys, 8, Q08005, doi:10.1029/2007GC001650.
Smirnov, A. V. (2009), Grain size dependence of low-temperature remanent magnetization in natural and synthetic magnetite: Experimental study, Earth Planets Space, 61, 119-124
Verwey, E.J. (1939), Electronic conduction of magnetite (Fe3O4) and its transition point at low temperature, Nature, 144, 327-328.
Verwey, E.J., P.W. Haayman, and F.C. Romeijn (1947), Physical properties and cation arrangements of oxides with spinel structure II. Electronic conductivity, J. Chem. Phys., 15, 181-187.
